今天看书看到了迪克斯特拉算法，大概用js实现一下呢，计算最短路径。

首先，迪克斯特拉算法只适用于有向无环图，且没有负权重，本例关系图如下哦，数字为权重，emmmm，画得稍微有点丑~

 

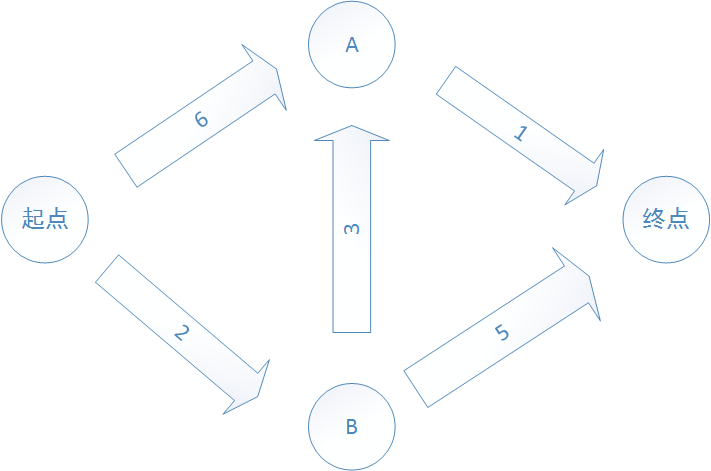
　　　　 //大概用js实现一下迪克斯特拉算法，计算最短路径        // （6）→ A → (1)        //   ↑    ↑    ↓        // 起点  (3)  终点        //   ↓    ↑    ↑        //  (2) → B → (5)        //迪克斯特拉算法只适用于有向无环图，且没有负权重        //上图()内为权重        //散列表在js中表示为对象        var graph = {};//记录节点        graph.start = {};        graph.start.a = 6;//起点到达A点权重为6        graph.start.b = 2;        graph.a = {};        graph.a.end = 1;        graph.b = {};        graph.b.end = 5;        graph.b.a = 3;        graph.end = {};        var costs = {};//记录起点到各点权重        costs.a = 6;        costs.b = 2;        costs.end = '';//暂时不知道        var parents = {};//记录最短路径中各节点的父节点        parents.a = 'start';        parents.b = 'start';        parents.end = '';        var processed = {};//记录已处理过的节点                //找出开销最小的节点(方法比较多呢，随便写了一个)        function findLowestCostNode(costs) {            var value = '';            var node = '';            for(var key in costs) {                if(processed[key]) {                    continue;                }                if(!value) {                    value = costs[key];                    node = key;                }else {                    if(costs[key] && costs[key]
     
       newCost) {
   //检查相应节点开销数是否小于已知开销数                        costs[n] = newCost;//更新相应节点开销数                        parents[n] = node;//更新相应节点父节点                    }                }            }            processed[node] = 1;;//记录已处理过节点            node = findLowestCostNode(costs);//更新最小节点继续循环        }        console.log(costs['end']);//6  此处为最短路径开销        var line = [];        line.unshift('end');        printLine(parents['end']);        console.log(line);//["start", "b", "a", "end"]        //使用递归打印出完整路径        function printLine(node) {            if( node != 'start') {                line.unshift(node);                printLine(parents[node]);            }else {                line.unshift('start');            }        }
     

看过的东西不使用就容易忘记，稍微记录一下，写法比较小白，大神们就自动忽略吧~

知道了新东西还真是一件有意思的事情~